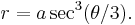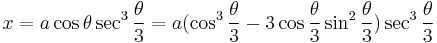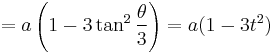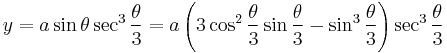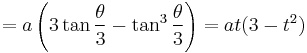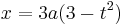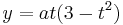Tschirnhausen cubic

In geometry, Tschirnhausen cubic, is a plane curve defined by the polar equation

r = a\sec^3(\theta/3).

Contents

History

The curve was studied by von Tschirnhaus, de L'Hôpital and Catalan. It was given the name Tschirnhausen cubic in a 1900 paper by R C Archibald, though it is sometimes known as de L'Hôpital's cubic or the trisectrix of Catalan.

Other equations

Put 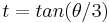t=tan(\theta/3). Then applying triple-angle formulas gives

x=a\cos \theta \sec^3 \frac{\theta}{3} = a(\cos^3 \frac{\theta}{3} - 3 \cos \frac{\theta}{3} \sin^2 \frac{\theta}{3}) \sec^3 \frac{\theta}{3}
= a\left(1 - 3 \tan^2 \frac{\theta}{3}\right)= a(1 - 3t^2)
y=a\sin \theta \sec^3 \frac{\theta}{3} = a \left(3 \cos^2 \frac{\theta}{3}\sin \frac{\theta}{3} - \sin^3 \frac{\theta}{3} \right) \sec^3 \frac{\theta}{3}
= a \left(3 \tan \frac{\theta}{3} - \tan^3 \frac{\theta}{3} \right) = at(3-t^2)

giving a parametric form for the curve. The parameter t can be eliminated easily giving the Cartesian equation

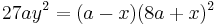27ay^2 = (a-x)(8a%2Bx)^2.

If the curve is translated horizontally by 8a then the equations become

x = 3a(3-t^2)
y = at(3-t^2)

or

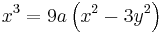x^3=9a \left(x^2-3y^2 \right).

This gives an alternate polar form of

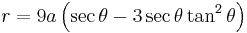r=9a \left(\sec \theta - 3\sec \theta \tan^2 \theta \right).

References

External links